Berekeningsgrondslagen industriestootdempers | B2B Shop

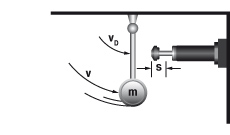
Ca. 90 % van de toepassingen kan aan de hand van de volgende vijf gegevens makkelijk worden berekend:

Af te remmen massa (gewicht) m [kg]
Stoot- of botssnelheid v_D [m/s]
Evt. aanwezige aandrijfkracht F [N]
Aantal slagen of cycli per uur x [1/h]
Aantal stootdempers parallel n

Bereken de juiste schokdemper voor uw toepassing

Gebruikte formuletekens

Afkorting	Unit	Beschrijving	Afkorting	Unit	Beschrijving
W₁	Nm	kinetische energie per slag; a.g.v. de massa	³HM	1 tot 3	aanloopkoppel factor (normaal 2,5)
W₂	Nm	energie van de aandrijfkracht per slag	M	Nm	aandrijfkoppel
W₃	Nm	totale energie per slag (W₁ + W₂)	J	kgm²	massatraagheidsmoment
¹W₄	Nm/h	totale energie per uur (W₃ · x)	g	m/s²	valversnelling = 9,81
me	kg	effectieve massa	h	m	valhoogte zonder stootdemperslag
m	kg	af te remmen massa	s	m	slaglengte stootdemper
n		aantal stootdempers (parallel)	L/R/r	m	straal
²v	m/s	snelheid bij de botsing	Q	N	reactiekracht
²v_D	m/s	botssnelheid opde stootdemper	μ		wrijvingscoëfficient
ω	rad/s	hoeksnelheid bij de botsing	t	s	afremtijd
F	N	aandrijfkracht	a	m/s²	vertraging
x	1/h	aantal slagen per uur	α	°	botshoek
P	kW	motorvermogen	β	°	hoek

¹ De in de bijbehorende vermogenstabellen vermelde toelaatbare W4-waarden gelden alleen bij kamertemperatuur. Bij hogere omgevingstemperaturen gelden lagere waarden.

² v resp. v_D is de eindsnelheid van de massa. Bij een versnellende beweging moet derhalve de gemiddelde snelheid met 50-100% verhoogd worden.

³ HM =^ verhouding tussen aanzetmoment en nominaal moment van de motor (afhankelijk van de bouwwijze)

De keuze van de stootdemper uit de capaciteitstabel volgt bij alle voorbeelden uit W3, W4, me en de geselecteerde stootdemperslag s.

Voor alle voorbeelden geldt:
Bij gebruik van meerdere dempers parallel worden de waarden W₃, W₄ en me door het aantal dempers gedeeld.

Reactiekracht Q [N]
Vooralle voorbeelden geldt:

Q = (1,5 · W₃) / s

Afremtijd t [s]
Vooralle voorbeelden geldt:

t = (2,6 · s) / v_D

Vertraging a [m/s2]
Vooralle voorbeelden geldt:

a = (0,75 · v_D²) / s

De formules voor de berekening van de reactiekracht, afremtijd en vertraging hebben alleen betrekking op industriestootdempers van ACE. Bij instelbare ACE industriestootdempers gelden deze3 formules alleen bij de juiste instelling. Hanteer een veiligheidsmarge. Bij veiligheidsstootdempers gelden andere formules. Neem hiervoor contact op met ACE.

Toepassingen

Toepassing	Formule	Voorbeeld
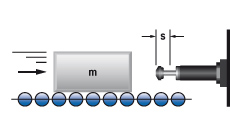
1. Massa zonder aandrijfkracht	W₁ = m · v² · 0,5 W₂ = 0 W₃ = W₁ + W₂ W₄ = W₃ · x v_D = v me = m	m = 100 kg v = 1,5 m/s x = 500 1/h s = 0,050 m (gekozen) W₁ = 100 · 1,5² · 0,5 = 113 Nm W₂ = 0 W₃ = 113 + 0 = 113 Nm W₄ = 113 · 500 = 56500 Nm/h me = m = 100 kg
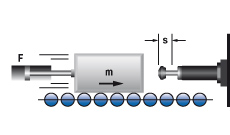
2. Massa met aandrijfkracht	W₁ = m · v2 · 0,5 W₂ = F · s W₃ = W1 + W2 W₄ = W3 · x v_D = v me = (2 · W₃) / v_D² 2.1 Bij verticale beweging omhoog W₂ = (F – m · g) · s 2.2 Bij verticale beweging omlaag W₂ = (F + m · g) · s	m = 36 kg ¹v = 1,5 m/s F = 400 N x = 1000 1/h s = 0,025 m (gekozen) W₁ = 36 · 1,5² · 0,5 = 41 Nm W₂ = 400 · 0,025 = 10 Nm W₃ = 41 + 10 = 51 Nm W₄ = 51 · 1000 = 51000 Nm/h me = 2 · 51 : 1,5² = 45 kg ¹ v is de eindsnelheid van de massa: Bij pneumatische: aandrij ving is daarom een verhoging van 50-100% de gemiddelde snelheid noodzakelij k..
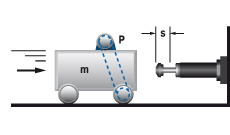
3. Massa met aandrijfkracht (geometrisch)	W₁ = m · v² · 0,5 W₂ = (1000 · P ·HM · s) / v W₃ = W₁ + W₂ W₄ = W₃ · x v_D = v me = (2 · W₃) / v_D²	m = 800 kg v = 1,2 m/s HM = 2,5 P = 4 kW x = 100 1/h s = 0,100 m (gekozen) W₁ = 800 · 1,2² · 0,5 = 576 Nm W₂ = 1000 · 4 · 2,5 · 0,1 : 1,2 = 834 Nm W₃ = 576 + 834 = 1410 Nm W₄ = 1410 · 100 = 141000 Nm/h me = 2 · 1410 : 1,2² = 1958 kg Opmerking: De rotatie-energie van motor, koppeling en transmissie, voor zover niet verwaarloosbaar, bij W₁optellen.
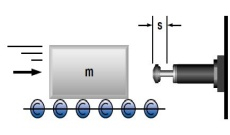
4. Massa op aangedreven rollen (met frictie)	W₁ = m · v² · 0,5 W₂ = m · μ · g · s W₃ = W₁ + W₂ W₄ = W₃ · x v_D = v me = (2 · W₃) / v_D²	m = 250 kg v = 1,5 m/s x = 180 1/h (Stahl/Guss) μ = 0,2 s = 0,050 m (gekozen) W₁ = 250 · 1,5² · 0,5 = 281 Nm W₂ = 250 · 0,2 · 9,81 · 0,05 = 25 Nm W₃ = 281 + 25 = 306 Nm W₄ = 306 · 180 = 55080 Nm/h me = 2 · 306 : 1,5² = 272 kg
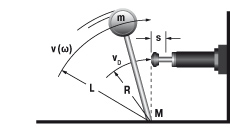
5. Zwenkende massa met aandrijfkracht	W₁ = m · v² · 0,5 = 0,5 · J · ω² W₂ = (M · s) / R W₃ = W₁ + W₂ W₄ = W₃ · x v_D = (v · R) / L = ω · R me = (2 · W₃) / v_D²	m = 20 kg v = 1 m/s M = 50 R = 0,5 m L = 0,8 m x = 1500 1/h s = 0,012 m (gekozen) W₁ = 20 · 1² · 0,5 = 10 Nm W₂ = 50 · 0,012 : 0,5 = 1,2 Nm W₃ = 10 + 1,2 = 11,2 Nm W₄ = 306 · 180 = 16800 Nm/h v_D = 1 · 0,5 : 0,8 = 0,63 m/s me = 2 · 11,2 : 0,63² = 56 kg
6. Massa in vrij e val	W₁ = m · g · h W₂ = m · g · s W₃ = W₁ + W₂ W₄ = W₃ · x v_D = √2 · g · h me = (2 · W₃) / v_D²	m = 30 kg h = 0,5 m x = 400 1/h s = 0,050 m (gekozen) W₁ = 30 · 0,5 · 9,81 = 147 Nm W₂ = 30 · 9,81 · 0,05 = 15 Nm W₃ = 147 + 15 = 162 Nm W₄ = 162 · 400 = 64800 Nm/h v_D = √2 · 9,81 · 0,5 = 3,13 m/s me = 2 · 162 : 3,13² = 33 kg
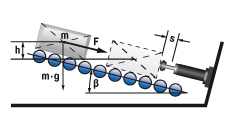
6.1 Massa op hellend vlak	W₁ = m · g · h = m · v_D² · 0,5 W₂ = m · g · sinβ · s W₃ = W₁ + W₂ W₄ = W₃ · x v_D = √2 · g · h me = (2 · W₃) / v_D² 6.1a Bij verticale beweging omhoog W₂ = (F – m · g· sinβ) · s 6.1b Bij verticale beweging omlaag W₂ = (F + m · g· sinβ) · s	m = 500 kg h = 0,1 m x = 200 1/h ß = 10 °C W₁ = 500 · 9,81 · 0,1 = 490,5 Nm W₂ = 50 · 9,81 · sin(10) · 0,075 = 63,9 Nm W₃ = 490,5 + 63,9 = 554,4 Nm W₄ = 554,4 · 200 = 11880,0 Nm/h
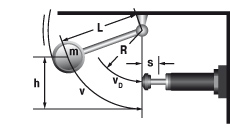
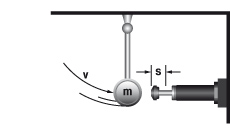
6.2 Massa vrij zwenkend	W₁ = m · g · h W₂ = 0 W₃ = W₁ + W₂ W₄ = W₃ · x v_D = √2 · g · h · (R / L) me = (2 · W₃) / v_D² tan α = s / R	m = 50 kg h = 1 m x = 50 1/h R = 300 mm L = 500 mm W₁ = 50 · 9,81 · 1 = 490,5 Nm W₂ = 0 W₃ = 490,5 + 0 = 490,5 Nm W₄ = 490,5 · 50 = 24525,0 Nm/h
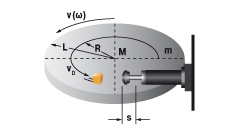
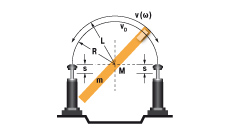
7. Draaitafel met aandrij fkoppel horizontaal of verticaal	W₁ = m · v² · 0,25 = 0,5 · J · ω² W₂ = (M · s) / R W₃ = W₁ + W₂ W₄ = W₃ · x v_D = (v · R) / L = ω · R me = (2 · W₃) / v_D²	m = 1000 kg v = 1,1 m/s M = 1000 Nm s = 0,050 m (gekozen) L = 1,25 m R = 0,8 m x = 100 1/h W₁ = 1000 · 1,1² · 0,25 = 303 Nm W₂ = 300 · 0,025 : 0,8 = 63 Nm W₃ = 28 + 9 = 366 Nm W₄ = 37 · 1200 = 36600 Nm/h v_D = 1,1 · 0,8 : 1,25 = 0,7 m/s me = · 366 : 0,7² = 1494 kg
8. Zwenkende massa met aandrijf-koppel (bij v. keer-inrichting)	W₁ = m · v² · 0,17 = 0,5 · J · ω² W₂ = (M · s) / R W₃ = W₁ + W₂ W₄ = W₃ · x v_D = (v · R) / L = ω · R me = (2 · W₃) / v_D²	J = 56 kgm² ω = 1 1/s M = 300 Nm s = 0,025 m (gekozen) L = 1,5 m R = 0,8 m x = 1200 1/h W₁ = 0,5 · 56 · 1² = 28 Nm W₂ = 300 · 0,025 : 0,8 = 9 Nm W₃ = 28 + 9 = 37 Nm W₄ = 37 · 1200 = 44400 Nm/h v_D = 1 · 0,8 = 0,8 m/s me = 2 · 37 : 0,8² = 116 kg
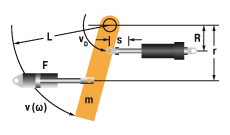
9. Zwenkende massa met aandrijfkracht	W₁ = m · v² · 0,17 = 0,5 · J · ω² W₂ = (F · r · s) / R = (M · s) / R W₃ = W₁ + W₂ W₄ = W₃ · x v_D = (v · R) / L = ω · R me = (2 · W₃) / v_D²	m = 1000 kg v = 2 m/s F = 7000 N M = 4200 Nm s = 0,050 m (gekozen) r = 0,6 m R = 0,8 m L = 1,2 m x = 900 1/h W₁ = 1000 · 2² · 0,17 = 680 Nm W₂ = 7000 · 0,6 · 0,05 : 0,8 = 263 Nm W₃ = 680 + 263 = 943 Nm W₄ = 943 · 900 = 848700 Nm/h v_D = 2 · 0,8 : 1,2 = 1,33 m/s me = 2 · 943 : 1,33² = 1066 kg
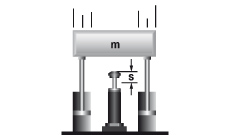
10. Massa zonder aandrijfkracht	W₁ =m · v2 · 0,5 W₂ = m · g · s W₃ = W₁ + W₂ W₄ = W₃ · x v_D = v me = (2 · W₃) / v_D²	m = 6000 kg v = 1,5 m/s s = 0,305 m (gekozen) x = 60 1/h W₁ = 6000 · 1,5² · 0,5 = 6750 Nm W₂ = 6000 · 9,81 · 0,305 = 17952 Nm W₃ = 6750 + 17 952 = 24702 Nm W₄ = 24702 · 60 = 1482120 Nm/h me = 2 · 24702 : 1,5² = 21957 kg

Toepassing

Formule

Voorbeeld

1. Massa zonder aandrijfkracht

Massa zonder aandrijfkracht ontmoet stootdemper

W₁ = m · v² · 0,5

W₂ = 0

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = v

me = m

m = 100 kg
v = 1,5 m/s
x = 500 1/h
s = 0,050 m (gekozen)

W₁ = 100 · 1,5² · 0,5 = 113 Nm
W₂ = 0
W₃ = 113 + 0 = 113 Nm
W₄ = 113 · 500 = 56500 Nm/h
me = m = 100 kg

2. Massa met aandrijfkracht

Masse mit Antriebskraft trifft auf Stoßdämpfer

W₁ = m · v2 · 0,5

W₂ = F · s

W₃ = W1 + W2

W₄ = W3 · x

v_D = v

me = (2 · W₃) / v_D²

2.1 Bij verticale beweging omhoog

W₂ = (F – m · g) · s

2.2 Bij verticale beweging omlaag

W₂ = (F + m · g) · s

m = 36 kg

¹v = 1,5 m/s

F = 400 N

x = 1000 1/h

s = 0,025 m (gekozen)

W₁ = 36 · 1,5² · 0,5 = 41 Nm

W₂ = 400 · 0,025 = 10 Nm

W₃ = 41 + 10 = 51 Nm

W₄ = 51 · 1000 = 51000 Nm/h

me = 2 · 51 : 1,5² = 45 kg

¹ v is de eindsnelheid van de massa: Bij pneumatische:
aandrij ving is daarom een verhoging van 50-100% de
gemiddelde snelheid noodzakelij k..

3. Massa met aandrijfkracht (geometrisch)

Masse mit Antriebskraft (formschlüssig) trifft auf Stoßdämpfer

W₁ = m · v² · 0,5

W₂ = (1000 · P ·HM · s) / v

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = v

me = (2 · W₃) / v_D²

m = 800 kg
v = 1,2 m/s
HM = 2,5
P = 4 kW
x = 100 1/h
s = 0,100 m (gekozen)

W₁ = 800 · 1,2² · 0,5 = 576 Nm
W₂ = 1000 · 4 · 2,5 · 0,1 : 1,2 = 834 Nm
W₃ = 576 + 834 = 1410 Nm
W₄ = 1410 · 100 = 141000 Nm/h
me = 2 · 1410 : 1,2² = 1958 kg

Opmerking: De rotatie-energie van motor, koppeling en
transmissie, voor zover niet verwaarloosbaar, bij W₁optellen.

4. Massa op aangedreven rollen (met frictie)

Masse ohne Antriebskraft trifft auf Stoßdämpfer

W₁ = m · v² · 0,5

W₂ = m · μ · g · s

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = v

me = (2 · W₃) / v_D²

m = 250 kg
v = 1,5 m/s
x = 180 1/h
(Stahl/Guss) μ = 0,2
s = 0,050 m (gekozen)

W₁ = 250 · 1,5² · 0,5 = 281 Nm
W₂ = 250 · 0,2 · 9,81 · 0,05 = 25 Nm
W₃ = 281 + 25 = 306 Nm
W₄ = 306 · 180 = 55080 Nm/h
me = 2 · 306 : 1,5² = 272 kg

5. Zwenkende massa met aandrijfkracht

Schwenkende Masse mit Antriebsmoment trifft auf Stoßdämpfer

W₁ = m · v² · 0,5 = 0,5 · J · ω²

W₂ = (M · s) / R

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = (v · R) / L = ω · R

me = (2 · W₃) / v_D²

m = 20 kg
v = 1 m/s
M = 50
R = 0,5 m
L = 0,8 m
x = 1500 1/h
s = 0,012 m (gekozen)

W₁ = 20 · 1² · 0,5 = 10 Nm
W₂ = 50 · 0,012 : 0,5 = 1,2 Nm
W₃ = 10 + 1,2 = 11,2 Nm
W₄ = 306 · 180 = 16800 Nm/h
v_D = 1 · 0,5 : 0,8 = 0,63 m/s
me = 2 · 11,2 : 0,63² = 56 kg

6. Massa in vrij e val

Frei fallende Masse trifft auf Stoßdämpfer

W₁ = m · g · h

W₂ = m · g · s

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = √2 · g · h

me = (2 · W₃) / v_D²

m = 30 kg
h = 0,5 m
x = 400 1/h
s = 0,050 m (gekozen)

W₁ = 30 · 0,5 · 9,81 = 147 Nm
W₂ = 30 · 9,81 · 0,05 = 15 Nm
W₃ = 147 + 15 = 162 Nm
W₄ = 162 · 400 = 64800 Nm/h
v_D = √2 · 9,81 · 0,5 = 3,13 m/s
me = 2 · 162 : 3,13² = 33 kg

6.1 Massa op hellend vlak

Masse auf schiefer Ebene trifft auf Stoßdämpfer

W₁ = m · g · h = m · v_D² · 0,5

W₂ = m · g · sinβ · s

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = √2 · g · h

me = (2 · W₃) / v_D²

6.1a Bij verticale beweging omhoog

W₂ = (F – m · g· sinβ) · s

6.1b Bij verticale beweging omlaag

W₂ = (F + m · g· sinβ) · s

m = 500 kg
h = 0,1 m
x = 200 1/h
ß = 10 °C

W₁ = 500 · 9,81 · 0,1 = 490,5 Nm
W₂ = 50 · 9,81 · sin(10) · 0,075 = 63,9 Nm
W₃ = 490,5 + 63,9 = 554,4 Nm
W₄ = 554,4 · 200 = 11880,0 Nm/h

6.2 Massa vrij zwenkend

Masse an Drehpunkt (frei schwingend) trifft auf Stoßdämpfer

W₁ = m · g · h

W₂ = 0

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = √2 · g · h · (R / L)

me = (2 · W₃) / v_D²

tan α = s / R

m = 50 kg
h = 1 m
x = 50 1/h
R = 300 mm
L = 500 mm

W₁ = 50 · 9,81 · 1 = 490,5 Nm
W₂ = 0
W₃ = 490,5 + 0 = 490,5 Nm
W₄ = 490,5 · 50 = 24525,0 Nm/h

7. Draaitafel met aandrij fkoppel horizontaal of verticaal

Drehtisch mit Antriebsmoment (horizontal oder vertikal) trifft auf Stoßdämpfer

W₁ = m · v² · 0,25 = 0,5 · J · ω²

W₂ = (M · s) / R

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = (v · R) / L = ω · R

me = (2 · W₃) / v_D²

m = 1000 kg
v = 1,1 m/s
M = 1000 Nm
s = 0,050 m (gekozen)
L = 1,25 m
R = 0,8 m
x = 100 1/h

W₁ = 1000 · 1,1² · 0,25 = 303 Nm
W₂ = 300 · 0,025 : 0,8 = 63 Nm
W₃ = 28 + 9 = 366 Nm
W₄ = 37 · 1200 = 36600 Nm/h
v_D = 1,1 · 0,8 : 1,25 = 0,7 m/s
me = · 366 : 0,7² = 1494 kg

8. Zwenkende massa met aandrijf-koppel (bij v. keer-inrichting)

Schwenkende Masse mit Antriebsmoment (z. B. Wendeeinrichtung) trifft auf Stoßdämpfer

W₁ = m · v² · 0,17 = 0,5 · J · ω²

W₂ = (M · s) / R

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = (v · R) / L = ω · R

me = (2 · W₃) / v_D²

J = 56 kgm²
ω = 1 1/s
M = 300 Nm
s = 0,025 m (gekozen)
L = 1,5 m
R = 0,8 m
x = 1200 1/h

W₁ = 0,5 · 56 · 1² = 28 Nm
W₂ = 300 · 0,025 : 0,8 = 9 Nm
W₃ = 28 + 9 = 37 Nm
W₄ = 37 · 1200 = 44400 Nm/h
v_D = 1 · 0,8 = 0,8 m/s
me = 2 · 37 : 0,8² = 116 kg

9. Zwenkende massa met aandrijfkracht

Schwenkende Masse mit Antriebsmoment (z. B. Wendeeinrichtung) trifft auf Stoßdämpfer

W₁ = m · v² · 0,17 = 0,5 · J · ω²

W₂ = (F · r · s) / R = (M · s) / R

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = (v · R) / L = ω · R

me = (2 · W₃) / v_D²

m = 1000 kg
v = 2 m/s
F = 7000 N
M = 4200 Nm
s = 0,050 m (gekozen)
r = 0,6 m
R = 0,8 m
L = 1,2 m
x = 900 1/h

W₁ = 1000 · 2² · 0,17 = 680 Nm
W₂ = 7000 · 0,6 · 0,05 : 0,8 = 263 Nm
W₃ = 680 + 263 = 943 Nm
W₄ = 943 · 900 = 848700 Nm/h
v_D = 2 · 0,8 : 1,2 = 1,33 m/s
me = 2 · 943 : 1,33² = 1066 kg

10. Massa zonder aandrijfkracht

Schwenkende Masse mit Antriebsmoment (z. B. Wendeeinrichtung) trifft auf Stoßdämpfer

W₁ =m · v2 · 0,5

W₂ = m · g · s

W₃ = W₁ + W₂

W₄ = W₃ · x

v_D = v

me = (2 · W₃) / v_D²

m = 6000 kg
v = 1,5 m/s
s = 0,305 m (gekozen)
x = 60 1/h

W₁ = 6000 · 1,5² · 0,5 = 6750 Nm
W₂ = 6000 · 9,81 · 0,305 = 17952 Nm
W₃ = 6750 + 17 952 = 24702 Nm
W₄ = 24702 · 60 = 1482120 Nm/h
me = 2 · 24702 : 1,5² = 21957 kg

Berekeningstool gebruiken en online bestellen

Effectieve massa (me)

De effectieve massa (me) is de werkelijke massa in beweging (voorbeeld A en C), deze massa vermeerderd met een theoretische massa uit aandrijfkracht of overbrenging (voorbeeld B en D).

Toepassing	Voorbeeld
A Massa zonder aandrijfkracht	m = 100 kg v_D = v = 2 m/s W₁ = W₃ = 200 Nm me = (2 · 200) / 4 = 100 kg Formule: me = m
B Massa met aandrijfkracht	m = 100 kg F = 2000 N v_D = v = 2 m/s s = 0,1 m W₁ = 200 Nm W₂ = 200 Nm W₃ = 400 Nm me = (2 · 400) / 4 = 200 kg Formule: me = (2 · W₃) / v_D²
C Massa zonder aandrijfkracht direct op de stootdemper	m = 20 kg v_D = v = 2 m/s W₁ = W₃ = 40 Nm me = (2 · 40) / 2² = 20 kg Formule: me = m
D Massa zonder aandrijfkracht met hefboomoverbrenging	m = 20 kg v = 2 m/s v_D = 0,5 m/s s = 0,1 m W₁ = W₃ = 40 Nm me = (2 · 40) / 0,5² = 320 kg Formule: me = (2 · W₃) / v_D²

Gebruikte formuletekens

Toepassingen

1. Massa zonder aandrijfkracht

2. Massa met aandrijfkracht

3. Massa met aandrijfkracht (geometrisch)

4. Massa op aangedreven rollen (met frictie)

5. Zwenkende massa met aandrijfkracht

6. Massa in vrij e val

6.1 Massa op hellend vlak

6.2 Massa vrij zwenkend

7. Draaitafel met aandrij fkoppel horizontaal of verticaal

8. Zwenkende massa met aandrijf-koppel (bij v. keer-inrichting)

9. Zwenkende massa met aandrijfkracht

10. Massa zonder aandrijfkracht

Effectieve massa (me)

A Massa zonder aandrijfkracht

B Massa met aandrijfkracht

C Massa zonder aandrijfkracht direct op de stootdemper

D Massa zonder aandrijfkracht met hefboomoverbrenging

ACE Stoßdämpfer GmbH | Inloggen